Quantum Computing: 2D Toric Codes and Surface Codes
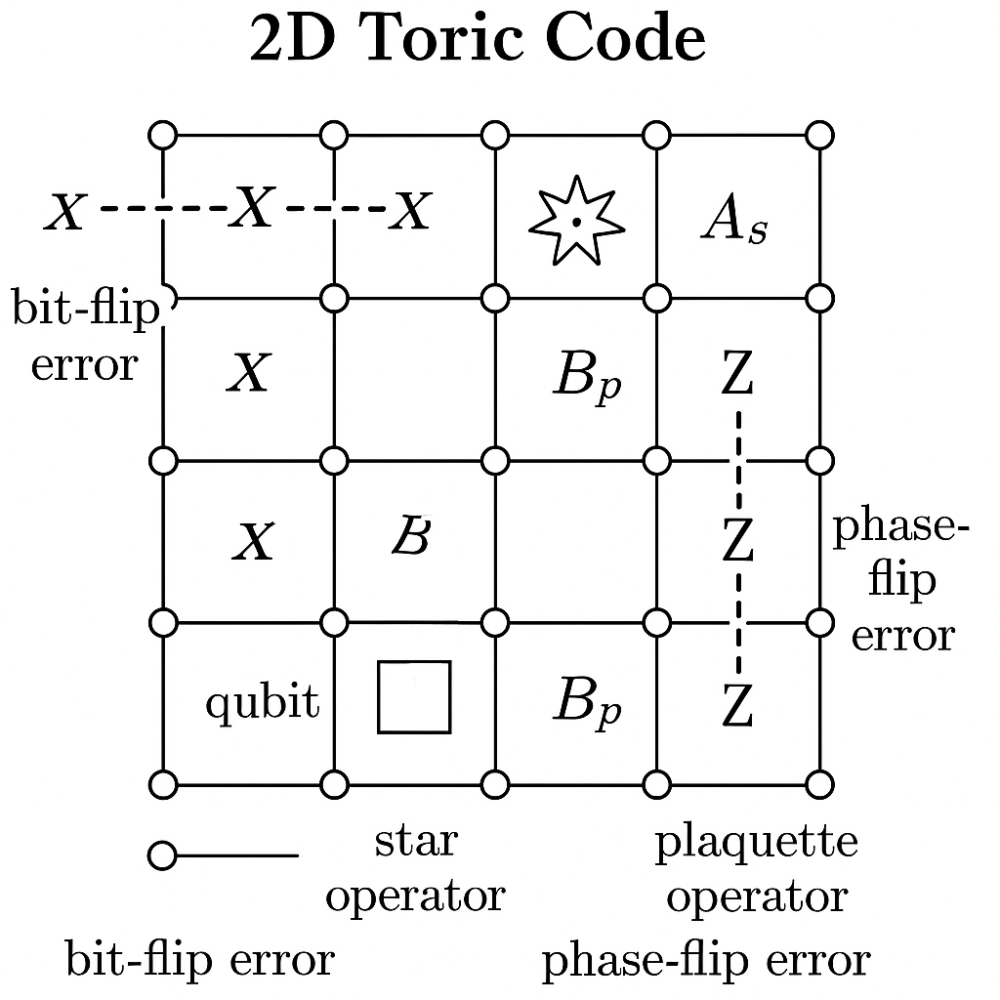
The 2D toric code is a foundational model in quantum error correction and topological quantum computing. It was introduced by Alexei Kitaev in 1997 as a way to protect quantum information from local noise by encoding it in global, topological degrees of freedom.
Structure of the Toric Code
- Imagine a square lattice drawn on the surface of a torus (a donut shape, hence the name “toric”).
- Each edge of the lattice hosts a qubit.
- Two types of operators (called stabilizers) act on sets of qubits: Star operators (A_s) act on the four edges meeting at a vertex.Plaquette operators (B_p) act on the four edges surrounding a face (plaquette).
- The code space is the subspace where all stabilizers return +1.
Error Detection
- Bit-flip errors (X errors): Detected by plaquette operators.
- Phase-flip errors (Z errors): Detected by star operators.
- Errors create pairs of anyonic excitations at the ends of error chains: Violated star → electric anyon (e)Violated plaquette → magnetic anyon (m)
- Moving an anyon across the lattice corresponds to applying a string of errors.
- Logical operations correspond to non-contractible loops around the torus—these can’t be detected locally.
Logical Qubits
- On an L × L lattice: There are 2 logical qubits encoded globally. Logical operators are loops of Pauli X or Z operators that wrap around the torus.
- The protection comes from the fact that to flip a logical qubit, an error must span the entire system—a long error chain that is exponentially unlikely if errors are local and independent.
Topological Features
- The toric code is an example of a topological quantum error-correcting code: It encodes information in global topology rather than local properties. Supports anyons with Abelian braiding statistics.
- It forms the basis for surface codes (planar versions with boundaries), which are widely used in today’s experimental quantum computing because they’re scalable and hardware-friendly.
Importance
- Practical: The surface code (derived from the toric code) is the leading error-correcting code in quantum computing platforms (e.g., superconducting qubits, trapped ions).
- Theoretical: It provides a concrete model for fault-tolerant quantum computation and a playground for anyon physics.
Application to Condensed Matter Physics
The 2D toric code and its relative, the surface code, play an important role not just in quantum information, but also in condensed matter physics. Researchers use them because they provide a simple, exactly solvable model of topological order (a state or phase of matter that arises in a system with non-local interactions), which is a central concept in modern condensed matter theory.
Here’s why they’re important in condensed matter physics:
1. Model of Topological Order
- The toric code is one of the simplest exactly solvable Hamiltonians that realizes topological order.
- Unlike conventional phases of matter (classified by local order parameters and symmetries, like in Landau’s theory), topologically ordered phases are characterized by: Long-range entanglement. Ground state degeneracy that depends on topology (e.g., torus vs. sphere).Exotic quasiparticles called anyons.
- The toric code provides a “toy model” that demonstrates all these features in a mathematically clean way.
2. Emergence of Anyons
- In the toric code, excitations above the ground state behave like anyons: Electric anyons (e).Magnetic anyons (m). Their fusion gives fermionic excitations (ε).
- These quasiparticles have Abelian braiding statistics (swapping them around changes the global quantum state in a way not possible with ordinary bosons/fermions).
- This makes the toric code an ideal playground for studying anyon physics, which is also relevant to real materials like the fractional quantum Hall effect.
3. Robust Ground State Degeneracy
- On a torus, the toric code has 4 degenerate ground states, independent of local details.
- This degeneracy is topologically protected—it can’t be lifted by any local perturbation.
- This property is analogous to what’s seen in real condensed matter systems with topological phases, where low-energy properties are insensitive to microscopic details.
4. Connection to Quantum Spin Liquids
- The toric code is closely related to models of quantum spin liquids, where spins remain highly entangled and disordered even at zero temperature.
- Kitaev’s honeycomb model (a more physical spin model) reduces to the toric code in a certain limit.
- This gives condensed matter physicists a way to study exotic phases of matter that don’t fit into conventional symmetry-breaking descriptions.
5. Bridge Between Physics and Quantum Computing
- In condensed matter, the toric code is studied as a phase of matter.
- In quantum information, it’s studied as an error-correcting code.
- The overlap shows a deep unity: the same mathematics that protects quantum memories also describes robust emergent phases in real materials.
In summary, condensed matter physicists use the 2D toric/surface code as a minimal, exactly solvable model of topological order to explore anyons, ground state degeneracy, quantum spin liquids, and robustness of topological phases. It serves as both a conceptual laboratory and a stepping stone toward understanding exotic states of matter found in experiments.
What are the differences between 2D Toric and Surface Codes?
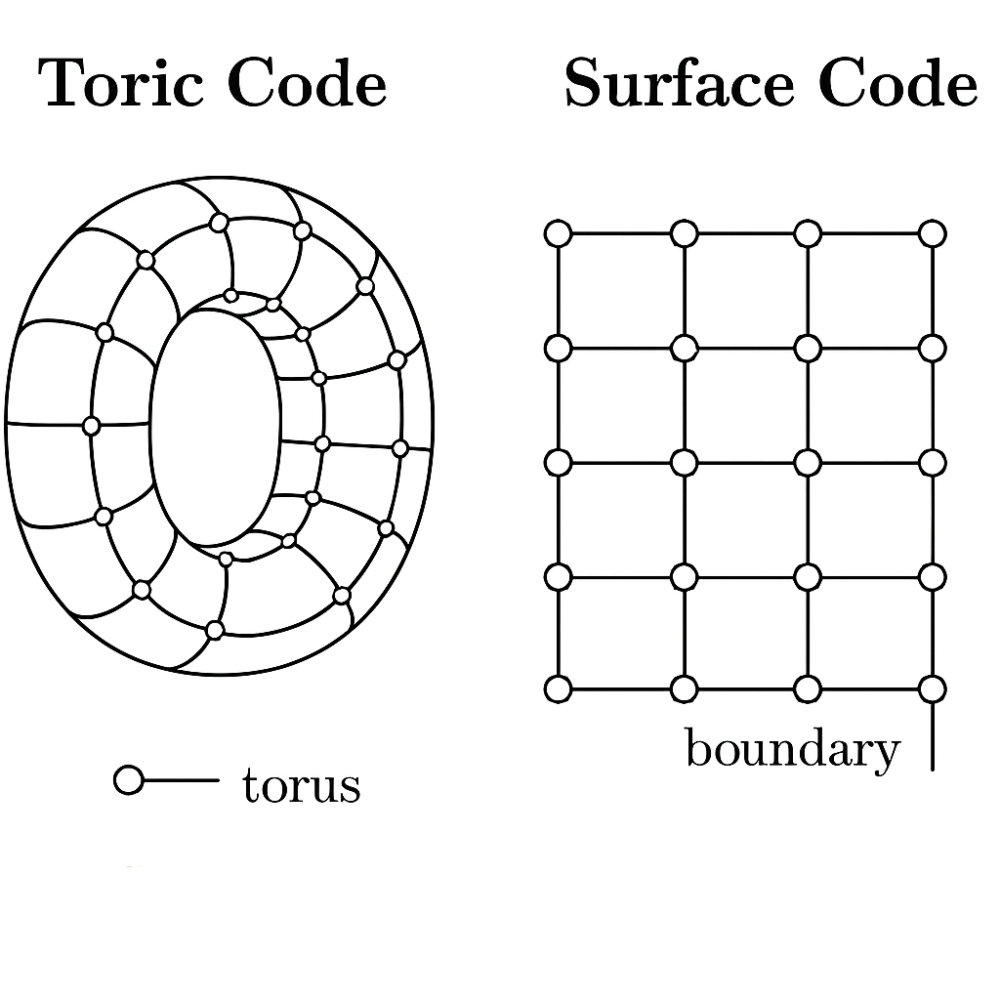
It is helpful to understand the difference between the 2D Toric code and the Surface code, and why one is more common in condensed matter physics, while the other dominates in quantum computing hardware.
Toric Code (Theory-Oriented)
- Setup: Qubits live on the edges of a square lattice. The lattice is wrapped onto a torus (donut shape), so there are no boundaries. This periodic boundary condition ensures clean topological properties (ground-state degeneracy tied to topology).
- Use in condensed-matter physics: It’s an exactly solvable Hamiltonian that realizes topological order. Provides a minimal model for studying anyons, braiding, and long-range entanglement.Elegant mathematically because the torus has no “edges” to complicate the physics.Good for exploring ground-state degeneracy and how it depends on the topology of the manifold (torus, sphere, etc.).
- Limitation: It’s hard to build an actual torus in the lab!Not directly implementable in physical qubit arrays — more of a conceptual model.
Surface Code (Practical-Oriented)
- Setup: Same lattice of qubits on edges, but placed on a planar (2D) surface with boundaries. Boundaries can be of two types: rough and smooth. Logical qubits are encoded using loops of errors connecting opposite boundaries, instead of loops around a torus.
- Use in quantum computing hardware: Can be realized on a flat chip (2D qubit array), which is scalable with superconducting qubits, trapped ions, Rydberg atoms, etc. The surface code has very high error thresholds (~1%), making it realistic for noisy devices. Supports fault-tolerant operations and active error correction using only nearest-neighbor interactions (hardware-friendly).
- Limitation: The topological structure is slightly less “clean” than the toric code (due to boundaries). Ground-state degeneracy depends on how you define the patch (edges vs holes).
Big Picture
- Condensed matter physicists prefer the toric code: it’s a pure theoretical model for exploring phases of matter and anyon statistics. Boundaries would complicate the neat classification of topological order.
- Quantum computing engineers prefer the surface code: It’s implementable on planar hardware, where qubits sit in a 2D grid. Boundaries allow for encoding logical qubits in a scalable architecture. It has the best-known balance of practical feasibility and robustness.
The toric code is the idealized, theoretical model for studying topological order in condensed matter, while the surface code is the practical, hardware-adapted version used for building real fault-tolerant quantum computers.