Mathematical representation

A superposition state is often represented as a linear combination of different basis states:

|ψ〉 = α |0⟩ + β |1⟩

where α and β are complex numbers, and |0⟩ and |1⟩ represent the two possible states of a qubit. The squared magnitudes of α and β, |α|2 and |β|2, gives the probabilities of measuring the qubit in state |0⟩ and |1⟩, respectively.

Nature of Superposition and How It Was Discovered

Mach-Zehnder Interferometer (UToronto)

The Mach-Zehnder interferometer, invented over one hundred years ago, is still used for optical measurements. “Mach” is the son, Ludwig, of the man, Ernst, who proposed Mach’s Principle and for whom a unit for the measurement of the speed of sound is named. Here we describe the details of how a simple version of the interferometer works; the discussion is largely non-mathematical but somewhat lengthy. A figure of the interferometer appears below.

The “legend” for the figure is:

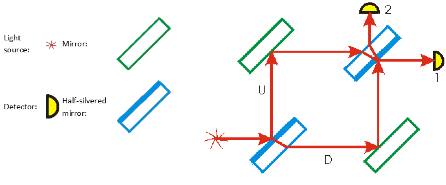
It turns out that, despite the figure, all of the light from the source ends up at detector 1; no light gets to detector 2.

The total difference between the two paths is that the U path has gone through one additional phase change of one-half a wavelength. There is complete destructive interference, and no light will reach detector 2. Detector 1 receives the complete constructive interference and all the light reaches detector 1.

Physical Embodiment and Measurement

Spin:

“Entanglement between photons and a quantum memory is a key component of quantum repeaters, which allow long-distance quantum entanglement distribution in the presence of fiber losses. Spin-photon entanglement has been implemented with a number of different atomic and solid-state qubits with long spin coherence times.” Two photons can be entangled in their spin, where one photon’s spin is always up while the other is always down. This is one example of spin entanglement of a quanta photon (Qubit) used in communications.

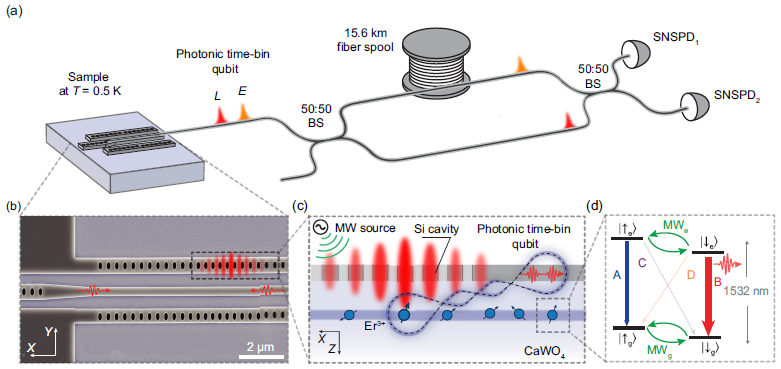
This diagram shows a more sophisticated Mach-Zehnder interferometer. A loop of fiber optic cable has been added to the “U” loop that delays the photon causing it to phase shift with the photon in loop “D”.

Er3+ : CaWO4 spin-photon interface.  (a) Optical setup used to generate and characterize spin-photon entanglement. Single photons entangled with the Er3+ ion and encoded in early (E) or late (L) time bins pass through a Mach-Zehnder interferometer (MZI) with a 15.6 km fiber spool in one arm and are detected at two superconducting nanowire single-photon detectors (SNSPDs). (b) Scanning electron microscope image showing a silicon nanophotonic cavity coupled to a bus waveguide, with a schematic of the resonant mode depicted in red. (c) Implanted erbium ions evanescently coupled to the silicon photonic crystal cavity placed on the surface of the CaWO4, and their spin transitions are driven by a microwave field. (d) Er3+ level structure in an applied magnetic field with four optical [(A)-(D)] and two microwave (MWc, MWg) transitions. The cavity resonance frequency is chosen to match the B transition, resulting in a larger Purcell enhancement for |↓e⟩(ΓB/ΓA =4.6).

Polarization:

Polarization, or polarisation, is a property of transverse waves which specifies the geometrical orientation of the oscillations. In a transverse wave, the direction of the oscillation is perpendicular to the direction of motion of the wave. Two photons can be entangled in their polarization, where if one is horizontally polarized, the other is vertically polarized.

An electromagnetic wave such as light consists of a coupled oscillating electric field and magnetic field which are always perpendicular to each other. Different states of polarization correspond to different relationships between polarization and the direction of propagation. In linear polarization, the fields oscillate in a single direction. In circular or elliptical polarization, the fields rotate at a constant rate in a plane as the wave travels, either in the right-hand or in the left-hand direction. When viewed in this way, the polarization of an electromagnetic wave is determined by a quantum mechanical property of photons called their spin. A photon has one of two possible spins: it can either spin in a right-hand sense or a left-hand sense about its direction of travel. Circularly polarized electromagnetic waves are composed of photons with only one type of spin, either right- or left-hand. Linearly polarized waves consist of photons that are in a superposition of right and left circularly polarized states, with equal amplitude and phases synchronized to give oscillation in a plane.

Mach-Zehnder Interferometer Use Examples:

The interferometer is used to measure the phase shift of a thin sample of, say, glass. The sample is placed in either the U or D beam. The phase shift of the sample alters the phase relationships between the two beams that we have just described, and there is no longer complete destructive interference at detector 2. Measuring the relative amount of light entering detector 1 and detector 2 allows a calculation of the phase shift produced by the sample. This phase shift is directly related to its refractive index.

Another example for this physical phenomenon is also used in the Mach-Zehnder Modulator employed in optical modems for fiber optic and free space communications. This diagram represents the MZM:

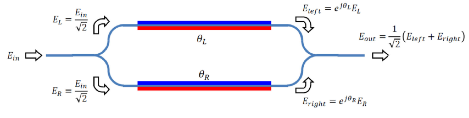
As in the interferometer the incoming light is split, experiencing phase shifts through the two paths and then recombined. If the phase shift between the two waves is 0°, then there is a maximum constructive interference, and the output intensity is highest (ideal logic 1). If the phase shift between the two waves is 180°, then there is maximum destructive interference, and the output intensity is lowest (ideal logic 0). An MZM changes the relative phase between the two paths with a modulation voltage via the electro-optic effect, producing a modulated output. The modulation in silicon is accomplished through silicon depletion-Mode or MOS capacitor accumulation-mode. The mathematical representation is shown in this formula:

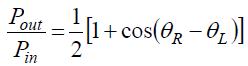
Why is this important?

In essence, quantum entanglement is a fascinating and counterintuitive phenomenon that highlights the bizarre nature of the quantum world, and its potential applications are still being explored. But understanding the nature of superposition and entanglement gives us an understanding of how qubits function. How quantum computers were conceived, are being developed and making them work.