Building a Quantum Computer

Research Quantum Computers

Chandelier quantum computers are research versions of a quantum computer designed and built to reduce interference as much as possible and ensure the most accurate results. The chandelier is encased in a cryostat, flooded with liquid helium to stabilize the electronics and qubit semiconductor chip to near zero degree absolute (0 Kelvin, -273.15 degrees Celsius, or -459.67 degrees Fahrenheit). At this temperature qubits, the quantum equivalent of bits, can be held more easily in superposition, allowing quantum computers to process information in parallel.

Why do pictures of quantum computers looks like some prop straight out of a sci-fi movie? Chandelier-style quantum computers are research tools identifying and testing approaches to developing quantum computers. These chandeliers allow the entire assembly to be lowered into a cryostat and flooded with liquid helium. These devices are not meant to be the industrial quantum computers we would use.

The chandelier also provides physical isolation from electromagnetic noise and unwanted signals. This isolation provides an operational environment that preserves the quantum superposition and entanglement. The quantum world is a very noisy place. Even so, qubits drop out of superposition and entanglement due to some kick of energy. We want to keep the qubit in superposition and entangled until measurement.

Quantum Computation

The fundamental principles of quantum computation establish the basic building blocks for quantum circuits and a universal language for describing sophisticated quantum computations. The two fundamental quantum algorithms known to date are constructed from circuits described in more detail below. We will examine quantum architecture, quantum gates, and quantum circuit models which are the fundamental building blocks of quantum computing. Quantum gates are universal, where any quantum computation can be expressed in terms of these gates.

Quantum Architecture

Fault-tolerant quantum computing (FTQC) is required because not all noise can be eliminated from a photonic system. FTQC requires more than 1,000,000 qubits to perform projective measurements. Single qubit rotations are hard to do, but entangling gates are easy. Developing a quantum architecture that is fault tolerant requires the unique properties of photons to encode and manipulate quantum information. It relies on a few key components and functionalities:

1. Qubit Encoding and Representation:

• Photonic quantum computing uses photons as the fundamental unit of information, qubits.
• Information can be encoded in various properties of the photon, such as polarization (e.g., horizontal or vertical) or path of travel (path encoding).
• Some approaches use qumodes, which are waves of light in an optical cavity, allowing for a broader range of quantum states.

2. Key Building Blocks:

• Quantum light sources: These generate single photons or entangled photon pairs, which are essential for creating and manipulating qubits.
• Photonic integrated circuits (PICs): These circuits contain optical waveguides and components that manipulate the photons’ quantum states, enabling quantum operations.
• Linear optical elements: Components like beam splitters and phase shifters are used to perform quantum operations on the photons.
• Single-photon detectors: These detectors measure the photons after they have been processed, allowing the computation results to be read out.
• Interferometers:These are a key building block used for qubit state preparation and projection, and to create quantum interference between photons.

3. Integration and Scalability:

• Integrated quantum photonics utilizes Photonic ICs (PICs) to miniaturize and scale up optical quantum circuits, moving away from bulk optics configurations.
• This approach offers advantages like reduced size, weight, and power consumption, as well as improved stability and manufacturability.
• However, integrating all the necessary components, including light sources, detectors, and control electronics, onto a single chip poses significant challenges, particularly for achieving high efficiency and fault tolerance.

4. Potential Advantages:

• Low decoherence: Photons are less susceptible to environmental noise compared to other qubit modalities.
• Room temperature operation: There is hope for some photonic quantum computers to operate at room temperature, reducing the need for complex cooling systems.
• High-speed operation: Photons travel at the speed of light, enabling fast quantum operations.
• Networking capabilities:Photonic qubits can be transmitted over long distances using optical fibers, facilitating quantum communication and networking.

5. Architectural Approaches:

• Discrete-variable (DV) photonic quantum computation: Focuses on encoding information in distinct modal properties like polarization and processing it with linear optical elements and single-photon detectors.
• Continuous-variable (CV) photonic quantum computation: Encodes information in continuous properties of the electromagnetic field and uses techniques like homodyne detection, a method of extracting information encoded as modulation of the phase and or frequency of an oscillating signal. By comparing the signal with a standard oscillation that would be identical to the signal if it carried null information. The Mach-Zehnder interferometer is used as a homodyne detector.

6. Importance of Fault Tolerance:

• For achieving fault-tolerant quantum computing, the architecture must address all aspects of qubit synthesis, control, and measurement, while being scalable indefinitely.
• Near-unit-efficiency single-photon detection is crucial for implementing fault-tolerant protocols.

In essence, a baseline photonic architecture for quantum computing involves generating quantum states with photons, manipulating them using integrated optical circuits, and detecting the results to perform quantum computations. While still a developing field, advancements in integrated photonics and materials science are pushing the boundaries of what is possible, paving the way for scalable and practical photonic quantum computers.

The Language of Quantum Mechanics in Quantum Computing

Quantum mechanics and quantum computing uses tensors, mathematical objects that generalize scalars, vectors, and matrices to higher dimensions. Basically, tensors are multi-dimensional arrays of number used to represent and manipulate data.  In addition, tensors are used in AI to perform mathematical operations. Vectors are a subset of tensors used in AI/Tensor flow Processors powering neural network deep-learning mathematical formalism. This mathematical formalism uses mainly a part of functional analysis, especially Hilbert spaces, which are a part of linear space. This mathematical formalism may be distinguished from the mathematical formalisms for physics theories developed prior to the early 1900s by the use of abstract mathematical structures, such as infinite-dimensional Hilbert spaces (L2 space mainly), and operators on these spaces. In brief, values of physical observables such as energy and momentum were no longer considered as values of functions on phase space, but as eigenvalues; more precisely as spectral values of linear operatorsin Hilbert space. The best book for understanding the application of mathematics to quantum physics is “Symmetries in Quantum Mechanics: From Angular Momentum to Supersymmetry” Masud Chaichian & Rolf Hagedorn, published by CRC Press, and Copy Righted in 1998 by Taylor & Francis Group, LLC.

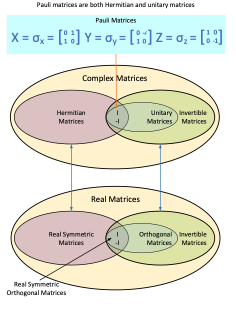
This diagram shows the relationship between the real and complex matrices spaces. We use both the real and complex symmetric matrices in quantum computing.

Hermitian matrices in Hilbert space: A† = A       where A† denotes the conjugate transpose.

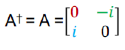
Matrix representation in a real vector space:

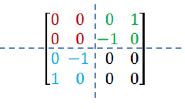
Without the conjugate condition, its equivalent real matrix is not symmetric.

The equivalent real matrix of a Hermitian matrix A† is a real symmetric matrix. A Hermitian matrix has the same properties as the real symmetric matrix, but all eigenvectors can be real or complex vectors.