Quantum Mechanics Applied to Quantum Computing – Quantum Algorithms
Quantum Algorithms
Many problems are impossible to solve on a classical computer, not because they are insoluble, but because of the astronomical resources required to solve realistic cases of the problems. The promise of quantum computers enables new algorithms that make feasible problems that would require exorbitant resources on a classical computer.
There are two broad classes of quantum algorithms that are known to fulfill this promise.
- The first class of quantum algorithms is based on Shor’s quantum Fourier Transform and includes algorithms for solving the factoring and discrete logarithm problems, providing a striking exponential increase in speed over the best-known classical algorithms.
- The second class of quantum algorithms is based on Grover’s algorithm for performing quantum searches. These provide a remarkable quadratic increase in speed over the best possible classical algorithms. These quantum algorithms are derived by adapting the classical algorithm to give a faster quantum algorithm.
Shor’s Algorithm
Shor’s algorithm leverages the principles of quantum mechanics, particularly superposition and interference, to explore multiple possibilities simultaneously when searching for the factors of a number. This parallel processing allows finding the period of a mathematical function much faster than classical computers, which must check possibilities one by one.
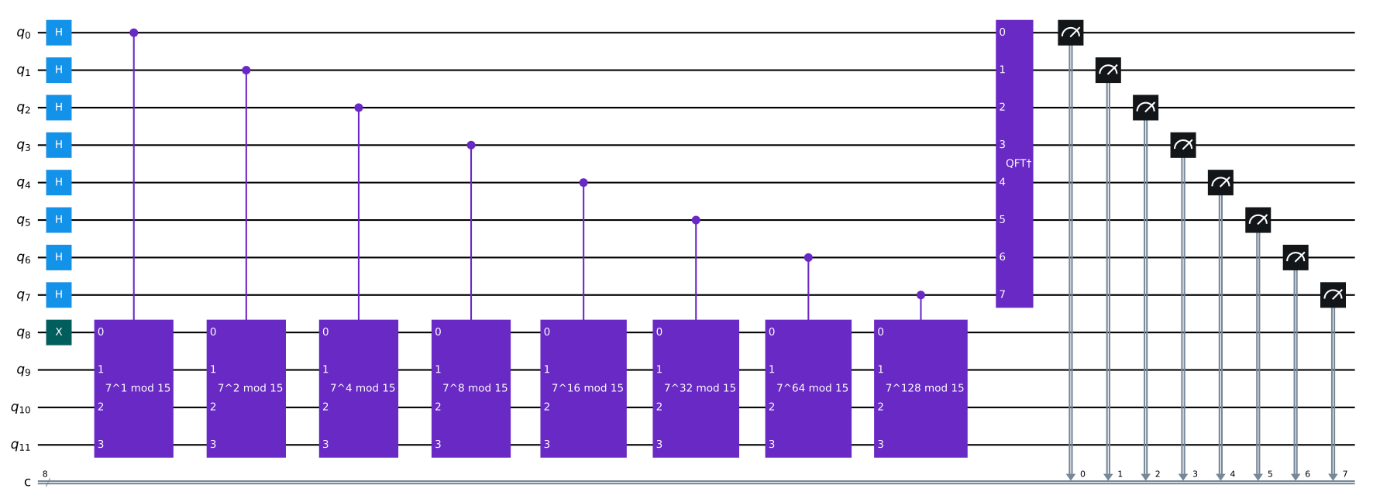
Shor’s algorithm quantum circuit (JavaFXpert, CC0, via Wikimedia Commons)
https://upload.wikimedia.org/wikipedia/commons/0/06/Shor%27s_algorithm_quantum_circuit.png
Significance:
- Computational Power:
Shor’s algorithm highlights the potential of quantum computers to solve problems that are intractable for classical computers.
- Security Implications:
Its ability to factor large numbers quickly raises concerns about the security of current encryption methods.
- Post-Quantum Cryptography:
The algorithm has driven research into post-quantum cryptography, seeking new encryption methods that are resistant to attacks from quantum computers.
Grover’s Algorithm
Grover’s algorithm is a quantum algorithm that provides a quadratic increase in speed in searching unsorted databases or solving unstructured search problems. It allows a quantum computer to find a specific item in a dataset in roughly the square root of the time it would take a classical computer.
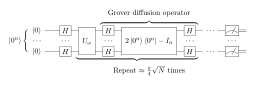
Fawly, CC BY-SA 4.0 <https://creativecommons.org/licenses/by-sa/4.0>, via Wikimedia Commons
https://upload.wikimedia.org/wikipedia/commons/b/b9/Grover%27s_algorithm_circuit.svg
Here’s a breakdown:
Core Idea:
- Grover’s algorithm leverages quantum superposition and interference to efficiently search a database.
- It uses an “oracle” (a function that identifies the solution) and a “diffusion operator” (which amplifies the probability of finding the solution).
- The algorithm iteratively applies these components to gradually increase the probability of finding the correct item.
Classical vs. Quantum Search:
- Classical:
In the worst-case scenario, a classical computer needs to check on average, half of the items in an unsorted list to find a specific element. Classical search algorithms are methods used in computer science and artificial intelligence to find a solution from a set of possible solutions. They systematically explore the search space, often using techniques like breadth-first search, depth-first search, or heuristic search, to locate the desired item or goal state
- Quantum (Grover’s):
Grover’s algorithm can achieve the same result with a number of operations roughly proportional to the square root of the number of items in the database (O(√N)). (IBM)
Key Concepts:
- Oracle:
A function that identifies the solution. It takes an input and returns 1 if it’s the correct item, and 0 otherwise.
- Diffusion Operator:
A quantum operation that amplifies the amplitude (probability) of the desired solution. - Superposition:
A quantum state where a qubit can represent multiple values simultaneously.
Applications:
- Database Search: Finding a specific record in an unsorted database.
- Optimization Problems: Finding the best solution from a set of possibilities.
- Machine Learning: Potential applications in reinforcement learning and classification tasks.
- Breaking Cryptographic Keys:While not breaking symmetric-key encryption like AES outright, it can reduce the effective key size, making it potentially easier to crack.
In essence, Grover’s algorithm provides a significant advantage in searching unsorted data, making it a valuable tool in the realm of quantum computing.
Quantum Computer Fault Tolerance and Noise Reduction
Because of the inherent nature of the quantum world, we need to talk about improving the performance of quantum computers in two major categories, noise reduction and fault tolerance. The impact of reducing noise and improving fault tolerance on a quantum computer has resulted in a diagram that is similar to the hardware/software protocol stack used in computer communications and software processing.
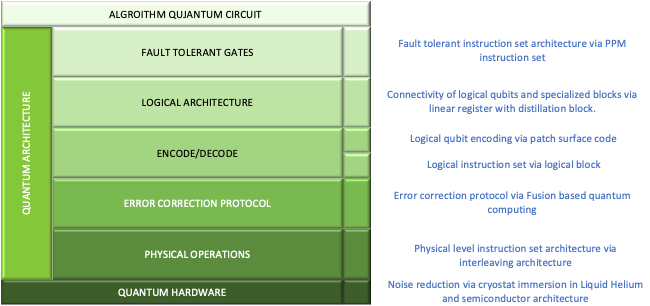
Quantum Error Correction Protocol Stack – Adapted from PsiQuantum Q2B Conference Presentation
As far as I know, Naomi Nickerson constructed this fault-tolerant protocol stack to detail the development of the necessary physical, architectural, and applications for various methods to reduce error/noise and computational faults. You can view her presentation to Q2B conference in Silicon Valley.
Noise Reduction
Some current approaches to reducing noise and faults in quantum computing involve combinations of techniques, including improving isolation, developing more robust qubit designs, and implementing quantum error correction methods. Researchers are also exploring noise-canceling techniques and novel fabrication methods to enhance superconducting qubits. Some approaches include:
1. Improving Isolation and Materials:
- Enhanced shielding:
Quantum computers are extremely sensitive to environmental noise (temperature fluctuations, electromagnetic fields, vibrations, etc.). Reducing this noise requires meticulous shielding and isolation of the qubits. - Cleanroom fabrication:
Utilizing advanced fabrication techniques in ultra-clean environments (like cleanrooms) minimizes the introduction of impurities that can act as noise sources. - Specialized materials:
Employing materials with specific properties to minimize noise interactions with qubits is a key area of research.
2. Robust Qubit Designs:
- Topological qubits:
These qubits are designed to be inherently resistant to local noise, as their quantum information is encoded in nonlocal properties through entanglement of qubits. - Superconducting qubits:
Researchers are developing new fabrication techniques for superconducting qubits that improve their noise resilience. - Noise-canceling qubits: Some research focuses on embedding “spectator qubits” to detect and cancel out noise affecting data-processing qubits. This can take an approach as noise cancelling or negative feedback to reduce noise.
3. Quantum Error Correction:
- Encoding information across multiple qubits:
Quantum error correction techniques encode quantum information across multiple entangled qubits, allowing for the detection and correction of errors without directly observing the qubit states to protect against errors caused by environmental noise or hardware imperfections. This involves encoding a single logical qubit into a larger entangled state of physical qubits, allowing for the detection and correction of errors without directly observing the qubits’ states. - Magic state distillation:
This technique involves creating high-fidelity quantum states from noisy ones, enabling the construction of fault-tolerant quantum computers. - Noise-aware compilation:
This involves optimizing quantum algorithms to be more resilient to noise and developing specialized algorithms like the Quantum Approximate Optimization Algorithm (QAOA).
4. Addressing Specific Noise Sources:
- Decoherence:
Understanding and mitigating decoherence, the loss of quantum information due to noise, is critical. - Dephasing:
Dephasing, which alters the phase of the quantum system’s wave function, is another noise source that needs to be addressed. - TLSs (Two-Level Systems):
These are defects in materials that can cause noise. Research aims to understand and eliminate them.
5. Other Approaches:
- Low-temperature operation:
Operating quantum computers at extremely low temperatures (millikelvins) significantly reduces environmental noise. - Noise-adaptive algorithms:
Algorithms are being developed that can dynamically adapt to the specific noise characteristics of a quantum system. - Virtual Z rotations:
This technique involves using software to simulate qubit rotations, reducing the need for physical rotations and minimizing errors.
By combining these strategies, researchers are making significant strides in reducing noise and improving the reliability of quantum computers, paving the way for more complex and powerful quantum computations.
____________________________________________________________________________
A note to my subscribers. This is the fourth in a series of seven articles about quantum computing and how quantum mechanics drives their development. We have an additional two subject areas we have developed touching on adapting artificial Intelligence (AI) to quantum computing. This subject delves deeply into how AI works and how it is processed on graphical processors using matrix mathematics. We analyze the complexity of this adaptation of AI to QCs through the use matrix mathematics and we look at a new development in QCs that starts to develop what is called Quantum AI.
The second subject area is the advanced development of semiconductor chip making driving to sub 1nm constructs, the advancements in the manufacturing of the chip making machines by ASML, and the use of very short wave ultraviolet optics to make these advances happen. The geometry of each transistor is now just a few atoms across, which presents some very interesting challenges, including powering these chips and dissipating their heat.
If you have any questions on these articles we have so far presented or need help in getting patents drafted and submitted to the USPTO or World Intellectual Property Organization (WIPO) countries, please feel free to reach out. I have submitted to both patent offices worldwide and know the challenges applicants face.