By Categories: AI & Technology, The Bleeding Edge

Quantum Mechanics Applied to Quantum Computing – Quantum Processing, Error Correction & Fault tolerance

Quantum Processing, Error Correction & Fault Tolerance

Error correction and fault-tolerance are areas of intensive development for quantum computing right now. These areas are necessary to get a quantum computer into production. Different companies are developing different approaches to this design challenge. Each company is developing their own quantum computer hardware/software protocol stack. I have adopted PsiQuantum, Naomi Nickerson’s Quantum Computer Hardware/Software Protocol stack as a workable architecture to discuss this rapidly developing area. I expect this protocol stack will evolve as the developers begin to bring down their QC error rates.

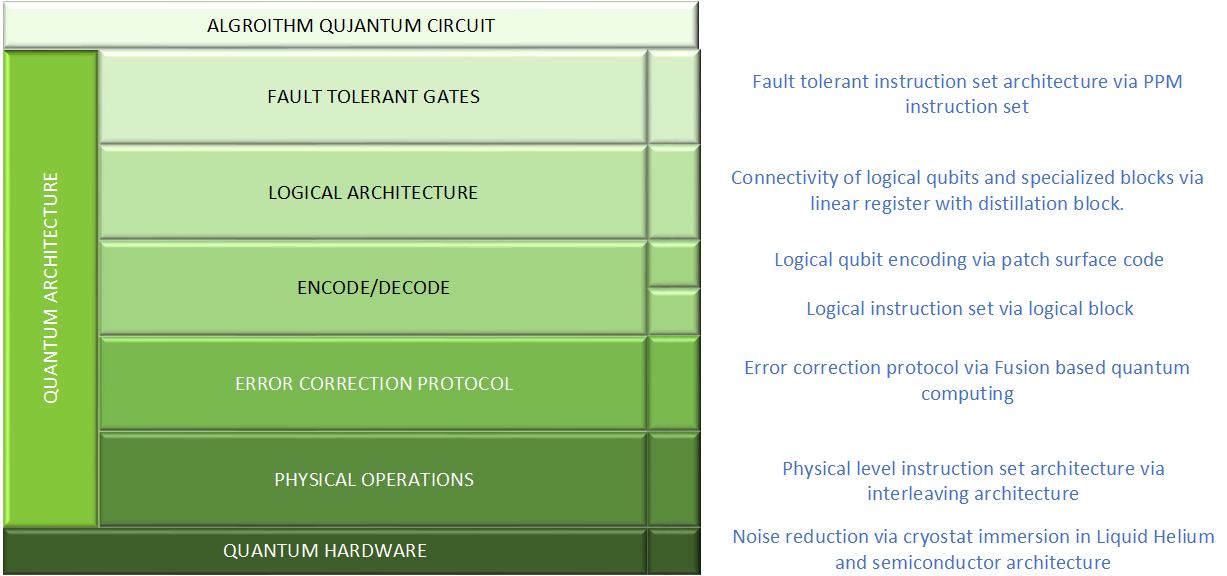
Current state-of-the-art quantum computers have error rates around 1% to 0.1%. To achieve fault tolerance, these error rates need to be significantly reduced, often below 0.1% or even much lower, to enable complex calculations. This means that, on average, one out of every 100 to 1000 operations will result in an error. To reduce the error rates logical qubits must be encoded across multiple physical qubits and error correction codes used to detect and correct errors.

The target error rate for fault-tolerant quantum computing is generally considered to be around parts in 106 or 1010, meaning that only one or fewer for every million to hundred million operations would be expected to have an error. Achieving this requires quantum error correction (QEC) and fault-tolerant architectures, which are crucial for mitigating the effects of noise and faulty components in quantum systems.

While significant progress has been made in demonstrating error correction, achieving fault tolerance at scale remains a major challenge. The overhead associated with QEC (the number of extra physical qubits needed for each logical qubit) can be substantial. However, research continues to explore more efficient QEC codes and architectures to reduce this overhead and make fault-tolerant quantum computing a reality.

Quantum Insider reported that Google’s Quantum AI-led team of researchers reported that they achieved a significant advance in quantum error correction (QEC). In a recent paper, published on the preprint server ArXiv, the researchers describe how they have achieved error rates below the critical threshold necessary for effective quantum error correction.

Quantum Gates and Quantum Error Correction

Qubits cannot be manipulated directly by programmers. Quantum gates are essential for quantum computing because they are the fundamental building blocks for manipulating qubits. Manipulating qubits enables quantum computers to perform complex computations that are impossible for classical computers. Quantum gates become the user interface to the qubits. They allow for the creation of quantum algorithms, quantum error correction, and other advanced quantum processes. Quantum gates operate probabilistically, taking advantage of quantum phenomena like superposition and entanglement.

Quantum error correction (QEC) uses quantum gates to protect quantum information from errors that inevitably occur in quantum computers. By encoding information across multiple physical qubits and employing specific quantum gate operations, QEC aims to detect and correct these errors, ultimately improving the reliability of quantum computations.

1. Encoding

Repetition Codes

A simple example is the three-qubit repetition code. A single logical qubit (the information you want to protect) is encoded into a three-qubit state. For example, the bit value ‘0’ might be encoded as ‘000’, and ‘1’ as ‘111’.

More Complex Codes

More sophisticated codes like the surface codeuse larger numbers of qubits and more complex entanglement patterns to achieve higher levels of error correction.

2. Error Detection and Correction

Parity Checks

Quantum gates, such as CNOT gates, are used to perform parity checks on the encoded qubits. These checks reveal information about the type and location of errors without directly measuring the encoded qubits. There are two fundamental types of quantum errors: bit flips and phase flips or a combination of both.

Bit flip errors occur when a qubit changes from |0⟩ to |1⟩ or vice versa. Bit flip errors are also known as σxerrors, because they map the qubit states σx|0⟩ = |1⟩ and σx|1⟩ = |0⟩. This error is analogous to a classical bit flip error.

Phase flip errors occur when a qubit changes its phase. They are also known as σz errors, because they map the qubit states σz|0⟩ = |0⟩ and σz|1⟩ = -|1⟩. This type of error has no classical analog.

Feedforward Control

Based on the parity checks, quantum gates (often single-qubit rotations) are applied to correct the errors. This process can involve real-time feedback loops where the results of measurements are used to guide subsequent gate operations. This open-loop approach compensates for the system’s dynamics and aims to maintain the integrity of logical qubits by actively responding to detected errors.

3. Fault-Tolerant Operations

Logical Qubits

QEC effectively creates “logical qubits” from multiple physical qubits. These logical qubits offer more robust protection against errors. Logical qubits are a higher-level abstraction of quantum information, built from multiple physical qubits to improve quantum computation’s reliability and stability. They are essential for performing complex quantum algorithms and achieving quantum advantage, as they mitigate the effects of noise and errors inherent in physical qubits.

Transversal Gates

Fault-tolerant quantum computation relies on transversal gates, which act on all qubits of a code block in the same way. This prevents the spread of errors during gate operations.

4. Key Challenges

Hardware Overhead

Hardware overhead in quantum error correction refers to the additional physical qubits needed beyond the logical qubits required for a computation. This overhead is necessary because quantum error correction relies on redundancy, using multiple physical qubits to encode a single logical qubit, which can then be used to detect and correct errors. The greater the required quantum computation accuracy, the more physical qubits are needed per logical qubit, thus increasing the hardware overhead. The number of physical qubits per logical qubit is determined by the error rate of the physical qubits and the desired logical error rate.

Gate Fidelity

The quantum gates used in the correction process must have high fidelity to avoid introducing new errors.

Scalability

Developing QEC schemes that can scale up to very large numbers of qubits remains a major challenge.

5. Recent Advances

  • Quantinuums Achievement:
    Quantinuum has demonstrated a universal, fully fault-tolerant gate set with repeatable error correction, a milestone deemed essential for scalable quantum computing according to The Quantum Insider.
  • Google’s Breakthrough:
    Google AI researchers have shown that error correction can reduce error rates in their superconducting qubit system according to the American Physical Society.
  • IBMs Work:
    IBM has published a landmark error correction paper that demonstrates the path towards running quantum circuits with a billion gates or more according to IBM.